来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/palindrome-number/
一、题目
给你一个整数 x ,如果 x 是一个回文整数,返回 true ;否则,返回 false 。
回文数是指正序(从左向右)和倒序(从右向左)读都是一样的整数。例如,121 是回文,而 123 不是。
示例 1:
输入:x = 121
输出:true
示例 2:
输入:x = -121
输出:false
解释:从左向右读, 为 -121 。 从右向左读, 为 121- 。因此它不是一个回文数。
示例 3:
输入:x = 10
输出:false
解释:从右向左读, 为 01 。因此它不是一个回文数。
示例 4:
输入:x = -101
输出:false
提示:
- -231 <= x <= 231 - 1
二、题解
解题源码: 链接
| \ | 时间复杂度 | 空间复杂度 |
|---|---|---|
| 字符串反转 | \ | \ |
| 数字反转 | \ | \ |
| 数字反转一半 | O(log n) | O(n) |
2.1.字符串反转
2.1.1.算法步骤
- 负数必然为 false
- 数字转字符串
- 反转字符串
- 字符串对比
2.1.2.动画演示
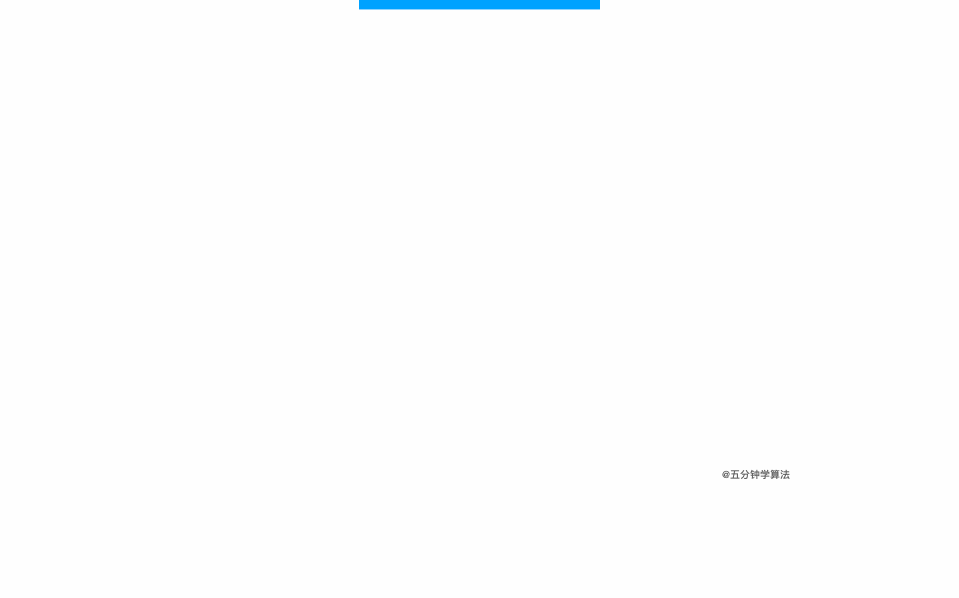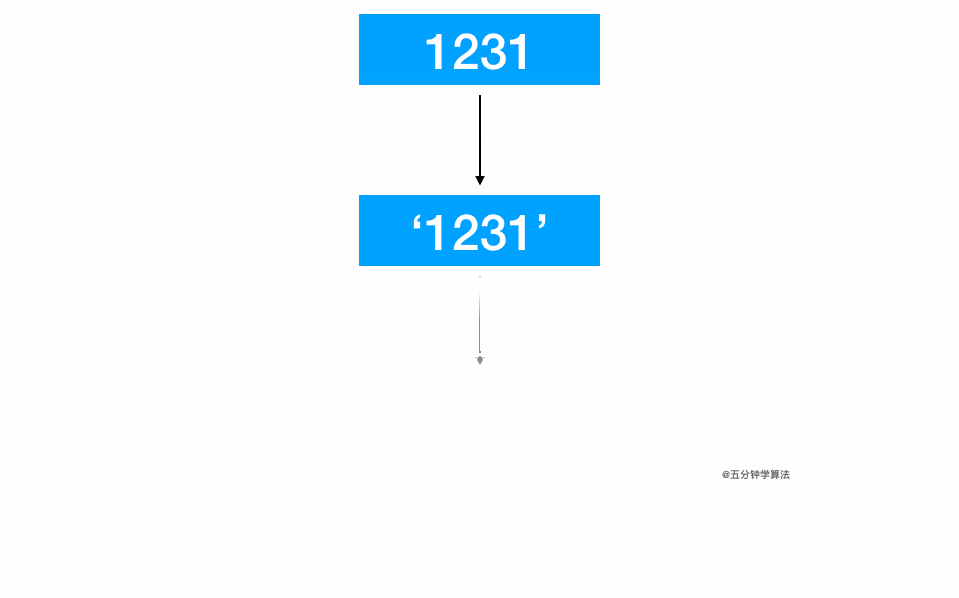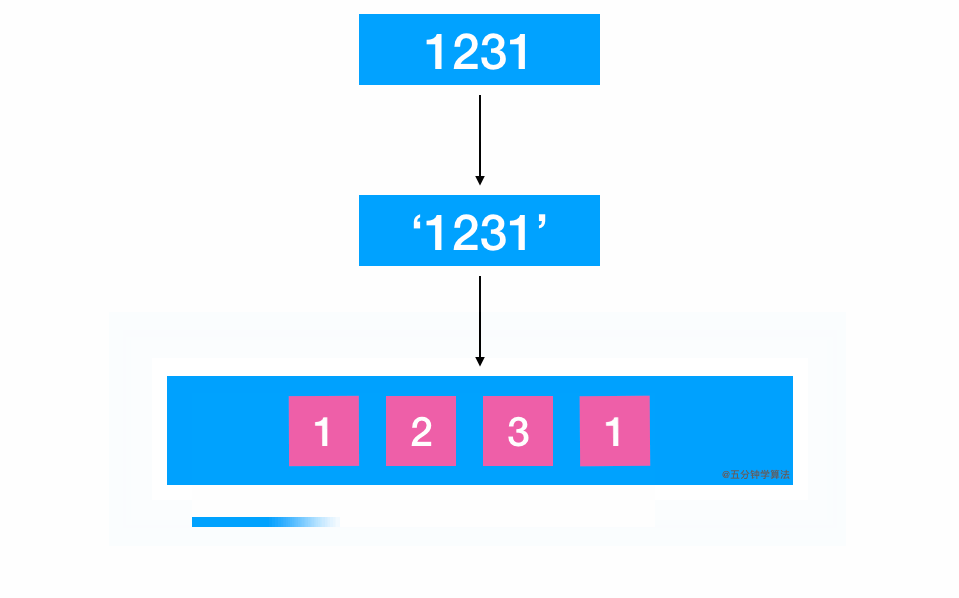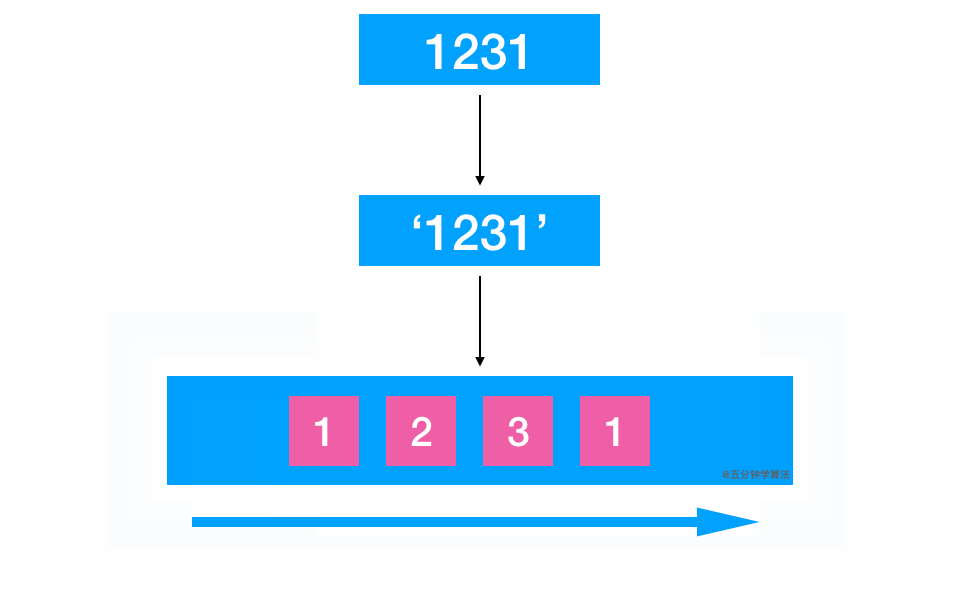
2.1.3.参考代码
解题源码: 链接
public class Id_0009_StringReverse implements Id_9 {
@Override
public boolean isPalindrome(int x) {
if (x < 0) return false;
String s = String.valueOf(x);
StringBuilder sb = new StringBuilder(s);
sb.reverse();
return s.equals(sb.toString());
}
}
2.2.数字反转
2.2.1.算法步骤
- 如果是负数则一定不是回文数,直接返回 false
- 如果是正数,则将其倒序数值计算出来,然后比较和原数值是否相等
- 如果是回文数则相等返回 true,如果不是则不相等 false
- 比如 123 的倒序 321,不相等;121 的倒序 121,相等
2.2.2.参考代码
解题源码: 链接
public class Id_0009_NumberReverse implements Id_9 {
@Override
public boolean isPalindrome(int x) {
if (x < 0 || (x % 10 == 0 && x != 0)) {
return false;
}
long cur = 0;
int num = x;
while (num != 0) {
cur = cur * 10 + num % 10;
num /= 10;
}
return cur == x;
}
}
2.3.数字反转一半
2.3.1.算法步骤
- 负数必然为 false
- 数字转字符串
- 反转字符串
- 字符串对比
2.3.2.动画演示
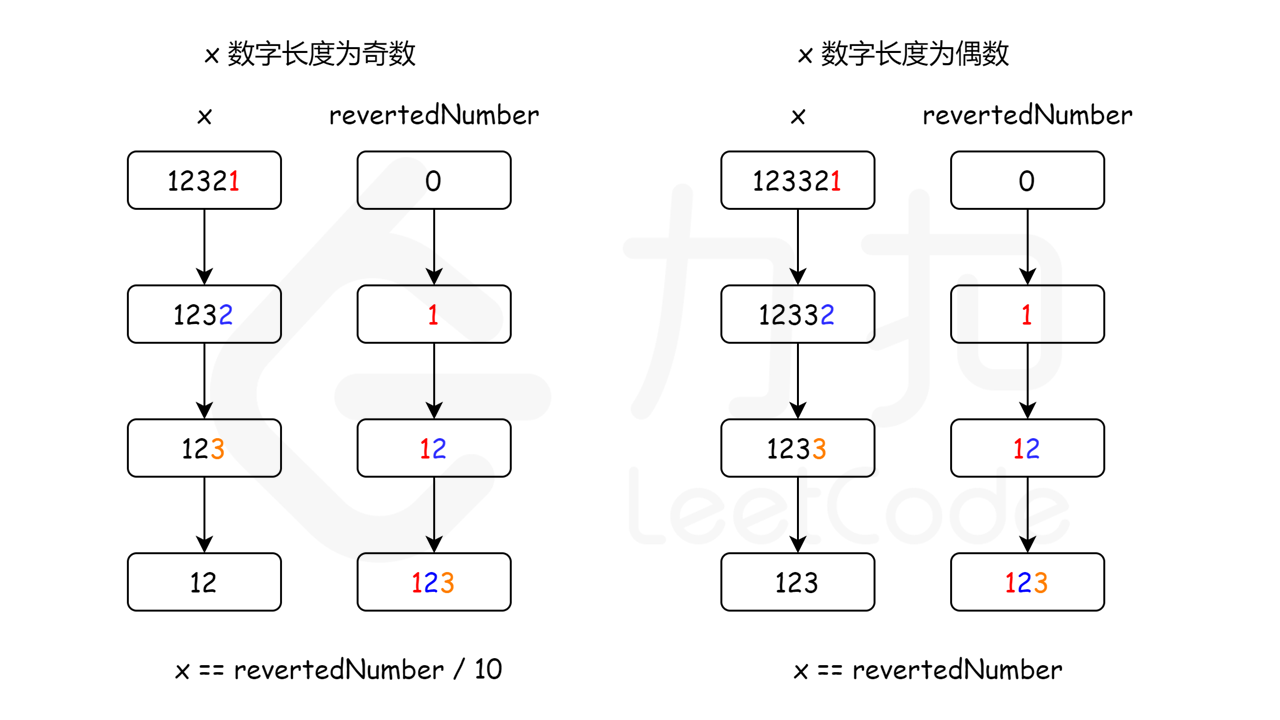
2.3.3.参考代码
解题源码: 链接
public class Id_0009_NumberReverseHalf implements Id_9 {
@Override
public boolean isPalindrome(int x) {
// 特殊情况:
// 如上所述,当 x < 0 时,x 不是回文数。
// 同样地,如果数字的最后一位是 0,为了使该数字为回文,
// 则其第一位数字也应该是 0
// 只有 0 满足这一属性
if (x < 0 || (x % 10 == 0 && x != 0)) {
return false;
}
int revertedNumber = 0;
while (x > revertedNumber) {
revertedNumber = revertedNumber * 10 + x % 10;
x /= 10;
}
// 当数字长度为奇数时,我们可以通过 revertedNumber/10 去除处于中位的数字。
// 例如,当输入为 12321 时,在 while 循环的末尾我们可以得到 x = 12,revertedNumber = 123,
// 由于处于中位的数字不影响回文(它总是与自己相等),所以我们可以简单地将其去除。
return x == revertedNumber || x == revertedNumber / 10;
}
}
参考:https://leetcode-cn.com/problems/palindrome-number/solution/dong-hua-hui-wen-shu-de-san-chong-jie-fa-fa-jie-ch/
参考:https://leetcode-cn.com/problems/palindrome-number/solution/hua-jie-suan-fa-9-hui-wen-shu-by-guanpengchn/
参考:https://leetcode-cn.com/problems/palindrome-number/solution/hui-wen-shu-by-leetcode-solution/ \
以上是个人学习记录,如有不正确请多多包涵,也欢迎评论告诉我,谢谢~


评论区